Simplistic Minimum Spanning Tree in Numpy [update]
I started working with spanning trees for euclidean distance graphs today.
The first think I obviously needed to do was compute the spanning tree.
There are MST algorithms in Python, for example in pygraph and networkx. These use their native graph formats, though, which would have meant I'd have to construct a graph from my point set.
I didn't see a way on how to do this and set the edge weights without iterating over all edges.
That would probably take longer than the computation of the MST, so I decided to do my own small implementation using numpy.
This is an instantiation of Prim's algorithm based on numpy matrices. The input is a dense matrix of distances, the output a list of edges. It is not as pretty as I would have hoped but still reasonably short. If any one has suggestions how to make this prettier, I'd love that.
[edit] Using line_profiler I had a quick look a the code and made some minor improvements. It's now significantly faster than networkx and also a bit prettier. Most time is now spent on the argmin, which seems reasonable. It would probably be even faster if I didn't use a full matrix for representing the weights but only the upper triangle. But that seems to be some extra effort.[/edit]
Here it goes:
All edges that connect nodes already inside the tree are set to infinity so as not to create cycles.
I haven't really benchmarked this and it probably loses against any cython implementation but I would hope it is reasonably fast and straight-forward.
The output looks something like this:
There are MST algorithms in Python, for example in pygraph and networkx. These use their native graph formats, though, which would have meant I'd have to construct a graph from my point set.
I didn't see a way on how to do this and set the edge weights without iterating over all edges.
That would probably take longer than the computation of the MST, so I decided to do my own small implementation using numpy.
This is an instantiation of Prim's algorithm based on numpy matrices. The input is a dense matrix of distances, the output a list of edges. It is not as pretty as I would have hoped but still reasonably short. If any one has suggestions how to make this prettier, I'd love that.
[edit] Using line_profiler I had a quick look a the code and made some minor improvements. It's now significantly faster than networkx and also a bit prettier. Most time is now spent on the argmin, which seems reasonable. It would probably be even faster if I didn't use a full matrix for representing the weights but only the upper triangle. But that seems to be some extra effort.[/edit]
Here it goes:
import numpy as np
from scipy.spatial.distance import pdist, squareform
import matplotlib.pyplot as plt
def minimum_spanning_tree(X, copy_X=True):
"""X are edge weights of fully connected graph"""
if copy_X:
X = X.copy()
if X.shape[0] != X.shape[1]:
raise ValueError("X needs to be square matrix of edge weights")
n_vertices = X.shape[0]
spanning_edges = []
# initialize with node 0:
visited_vertices = [0]
num_visited = 1
# exclude self connections:
diag_indices = np.arange(n_vertices)
X[diag_indices, diag_indices] = np.inf
while num_visited != n_vertices:
new_edge = np.argmin(X[visited_vertices], axis=None)
# 2d encoding of new_edge from flat, get correct indices
new_edge = divmod(new_edge, n_vertices)
new_edge = [visited_vertices[new_edge[0]], new_edge[1]]
# add edge to tree
spanning_edges.append(new_edge)
visited_vertices.append(new_edge[1])
# remove all edges inside current tree
X[visited_vertices, new_edge[1]] = np.inf
X[new_edge[1], visited_vertices] = np.inf
num_visited += 1
return np.vstack(spanning_edges)
def test_mst():
P = np.random.uniform(size=(50, 2))
X = squareform(pdist(P))
edge_list = minimum_spanning_tree(X)
plt.scatter(P[:, 0], P[:, 1])
for edge in edge_list:
i, j = edge
plt.plot([P[i, 0], P[j, 0]], [P[i, 1], P[j, 1]], c='r')
plt.show()
if __name__ == "__main__":
test_mst()
The algorithms basically works on a dense distance matrix and finds the best possible edge that
is reachable from a set of active nodes.All edges that connect nodes already inside the tree are set to infinity so as not to create cycles.
I haven't really benchmarked this and it probably loses against any cython implementation but I would hope it is reasonably fast and straight-forward.
The output looks something like this:
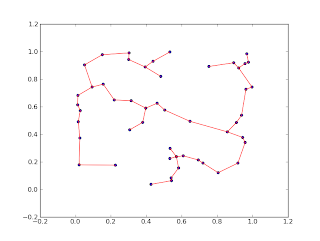



Thanks for the update! Looks great, I am using your code in my class!
ReplyDeleteCool. :-) what class is that?
DeleteHello. I need kruskal code. could you please send it to my email adrress: elfetop2012@yahoo.com. best wishes
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteDid this turn out not to be true? Sorry for the slow reply :-/
Deleteis there a possibility to solve it in parallel or in GPU using pycuda
ReplyDeleteI would not recommend it. This algorithm is super serial. Also, I would rather go for Cython. The algorithm is super fast in principal, that is O(|E| log |V|) if you are careful. How big is your graph?
DeleteCan you Help me how can I code the Relative Neighborhood Graph using PYTHON.
ReplyDeleteMy input data is a distance matrix between nodes.
ReplyDelete